G h at height h above the surface of the earth. Therefore acceleration due to gravity decreases with increase in depth.

Draw A Graph Showing The Variation Of Gravitational Acceleration Due To The Depth And Altitude From Brainly In
G d 43 πρ R d G.
. G Slope of Vs graph g 4 π 2 Slope of T 2 Vs l graph. When object is at depth. Height above the earths surface and depth below the earths surface.
Choose suitable scales on these axes to represent L and T2 or T. F M1 x 667408 10-11 x 7349 x 1022 174x1062 or. Avail 25 off on study pack.
G 43 πρRG. R - d. And here is the acceleration-time graph for a freely falling object.
Now it has been proven that the acceleration due to gravity increases uniformly till a distance equal to the radius of the earth where it becomes highest and then decreases exponentially. Draw graphs of showing the variation acceleration due to gravity withheight above the earths surface anddepth below the earths surface. Acceleration acceleration due to gravity g 10 ms2.
H 120 R gh 9 ms 2 Radius of earth R 6400 km. The weight of a body on the surface of earth is 2 5 0 N. And g2 is the acceleration due to gravity at depth d with respect to the earths surface.
Calculate its weight at distance equal to half of the radius of earth below the surface of earth. Starting early can help you score better. Hard Solution Verified by Toppr aThe value of g varies with height as g Rh1 2 or g r 21 b The value of g varies with depth as g d g1 Rd g d Rd Solve any question of Gravitation with-.
BThe variation of g with depth is released by equation gg 1-dR ie. G G M E R E 2. 0 Maharashtra State Board HSC Science Computer Science 11th.
Thus the variation of g and r is a parabolic curve. If g is the acceleration due to gravity at depth d Let the Earth be of uniform density r and its shape be a perfect sphere. The slope has UNITS and those units should be those of acceleration.
This slope is found to be constant at a place and is equal to g 4 π 2 g where g is the acceleration due to gravity at that place. Draw a graph showing the variation of gravitational acceleration due to the depth and altitude from the Earths surface. First we will see the variation of acceleration due to gravity.
Acceleration due to gravity. A The acceleration due to gravity g fracmathrmGMmathrmr2 This equation shows that acceleration is indepent of mass of body that falls to the earth. Variation of g with depth is expressed by the formula g2 g 1 dR.
Take effective length L along the x-axis and T2 or T along the y-axis using the observed values from the table. Determine v o from your graph v o is the v-intercept. Given the radius of the earth 6400 km.
The rule with a Δ notation. Hence from the origin to the point r98 graph will be a straight line and after the point r98 the graph will decrease exponentially tending to zero as distance tends to infinity. When object is at attitude from surface of Earth.
At a distance d below the earths surface the acceleration due to gravity is given by. Thus g can be determined at a place from these measurements using the following relation. G GMR2 1 If g h is the acceleration due to gravity at a pt situated at a height h above the surface of the earth.
The acceleration due to gravity at a height 120 th radius of the earth above the earths surface is 9 ms 2. Expanding Binomially and neglecting higher power. If we go deeper g decreases.
Hence earth impart same acceleration on all bodies. G on the surface of the earth is given by. F M1 x 16 kg x ms-2 kilogram meters per second squared So the force of gravity one feels on the surface of the Earth is 98 times their mass and the force of gravity one feels on the Moon is 16 times their mass.
How will you use this graph to determine the value of g acceleration due to gravity 2 See answers Advertisement Advertisement DiptayanBanerjee DiptayanBanerjee Answer. Here g1 is the acceleration due to gravity at a height of h with respect to the earths surface. If mass m is placed at depth d the whole mass of earth doesnt attracts the mass m Rather only the inner solid sphere apply.
Find the value of acceleration due to gravity at an equal distance below the surface of the earth. Radius of earth 6 4 0 0 k m. Hence its a uniformly accelerated motion.
In this Physics video lecture in Hindi for class 11 we explained how acceleration due to gravity g varies with depth. This is a second way of determining the acceleration due to gravity. Selected Aug 28 2018 by faiz.
Acceleration-time graph for a freely falling object. Record this value of g in your results and compare to the accepted value and to the average value of g obtained in the table. When the depth d 0 the value of g on the surface of the earth g d g.
So the graph showing variation of acceleration due to gravity and height would be. Selected Nov 17 2018 by faiz. Just work them out from the basic recipe.
Drawn the required graph is drawn. G R-d Thus the variation of g and d is a straight line. In such cases distance between earth and object changes which lead to change in value to g ie.
AThe variation of g with height h is related by relation g 1r2 where rRh. Then add an extra extra distance DC where DC aΔt 2. Graph is given in the attachment.
Plot a graph showing the variation of acceleration due to gravity with the center of the earth. We derived 3 equations related to this quantity Details here Eq87. Slope PR QR ab cd PR QR ab cd T 1 2 - T 2 2 l 1 - l 2.
G h G M E R E h 2. Here the free-fall a vertical motion of the object happens in a uniform gravitational field. Take the graph AB as found at the last interval and run on AB straight to D as if there were no acceleration.
Then BC is the next bit of graph. Where r is the density of the Earth Comparing g and g. Draw a graph showing the variation of t2 with L.
If the acceleration should vary the extra extra distances like DC will vary. Pls mark my answer as Brainliest. Draw graphs showing the variation of acceleration due to gravity with a height above the earths surface b depth below the earths surface.
On dividing the above equations we get g d g R dR. Plot a graph between L and T2 as shown in figure 2 and also between L and T as shown in figure 1. Acceleration due to gravity at the surface of the earth.
The Variation Of Acceleration Due To Gravity G With Distance D From Centre Of The Earth Is Best Represented By R Earth S Radius Sarthaks Econnect Largest Online Education Community
What Is The Graph Of Acceleration Due To Gravity From The Center Of The Earth To Infinity Quora

Draw Graphs Showing The Variation Of Acceleration Due To Gravity With A Height Above The Earth S Surface B Depth Below The Earth S Surface
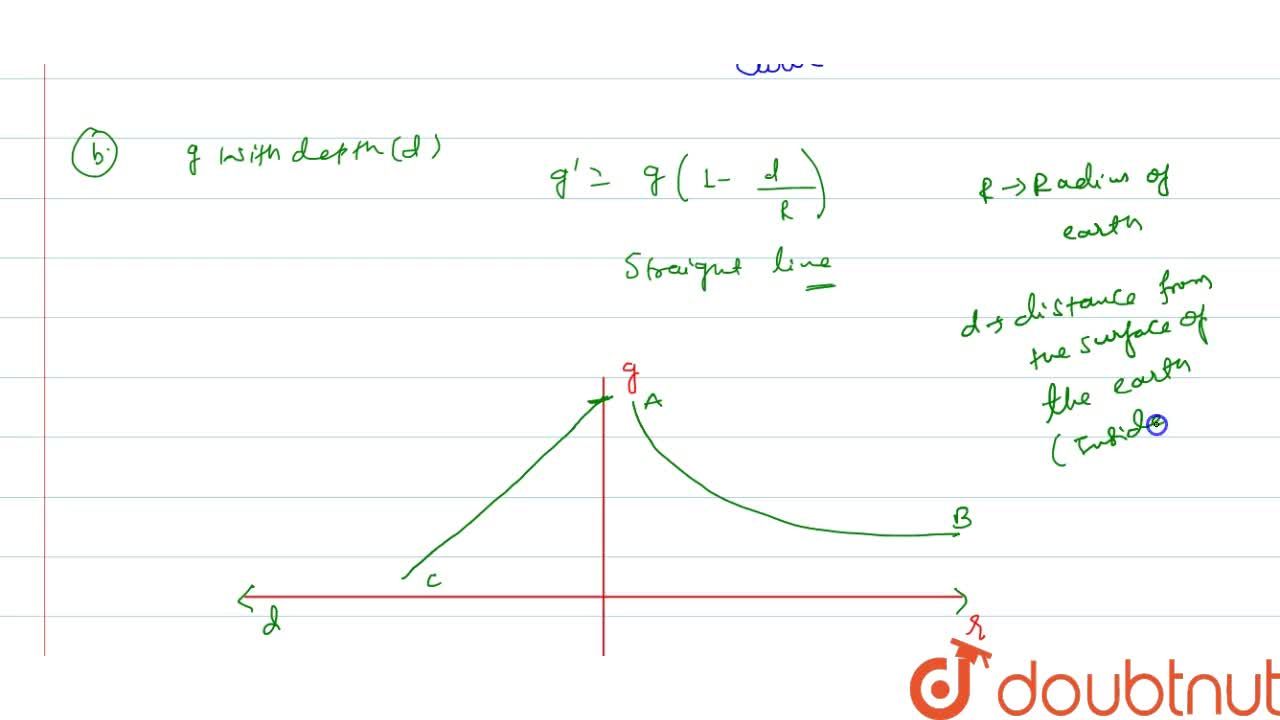
Draw Graphs Showing The Variation Of Accleeration Due To Gravity With A Height Above The Earth S Surface B

Plot A Graph Showing The Variation Of Acceleration Due To Gravity With The Distance From The Centre Of The Earth

Solve This Q Draw The Graph Showing The Variation Of Acceleration With Heigh Above The Earth Surface And Physics Gravitation 11991881 Meritnation Com

Answer The Following Question In Detail Draw A Graph Showing The Variation Of Gravitational Acceleration Due To The Depth And Altitude From The Earth S Surface Physics Shaalaa Com

Plot A Graph Showing The Variation Of Acceleration Due To Gravity With The Center Of The Earth The Weight Of A Body On The Surface Of Earth Is 250 N Calculate
0 comments
Post a Comment